TAMANHO ÓTIMO DE PARCELAS PARA EXPERIMENTOS COM POEDEIRAS PELO MÉTODO DA COMPARAÇÃO DAS VARIÂNCIAS

OPTIMUM SIZE OF PLOTS FOR LAYING HENS EXPERIMENTS BY THE VARIANCE COMPARISONMETHOD

ABSTRACT - In view of the importance of experiments in poultry farming and the need to use the appropriate size of plots, this study was carried out to determine the size of plots for experiments with laying hens, based on several published papers in the area in the last ten years. In order to do so, the plot sizes and number of replications were used, as well as the variation coefficients found in each one. From these experimental data, the ideal sizes were calculated for each evaluated variable using the comparing variances method. Several plot sizes were found and evaluated, in which each animal was first considered as a basic unit (plot) up to 10 animals per basic unit

---

Introdução

Independente do material experimental que se utiliza e do ambiente onde será realizada a experimentação, o planejamento experimental deve ser feito com a finalidade de reduzir o erro experimental. Uma medida de erro experimental é a existente entre unidades experimentais que receberam o mesmo tratamento, a qual é estimada mediante a utilização da repetição, um dos princípios da experimentação (STORCK et al., 2006). As estimativas de tamanho de parcela, efetuadas para diferentes animais possibilita verificar a sua variação com espécie, raça, local, idade, característica avaliada, número de animais utilizados na unidade básica, época da avaliação, forma da parcela e método utilizado para a sua estimativa. Diante da importância dos experimentos na área de avicultura e da necessidade de se utilizar o tamanho adequado de parcelas. Objetivou-se determinar o tamanho ótimo de parcelas para experimentos com poedeiras comerciais, utilizando-se o método da máxima curvatura e o método da máxima curvatura modificado.

---

Revisão Bibliográfica

O Brasil se destaca no setor de avicultura de postura possuindo a maior indústria de produção de ovos da América Latina e sétima maior do mundo (USDA, 2014). O país alcançou, no segundo trimestre deste ano, a maior produção de ovos de galinha desde o início da série histórica da pesquisa que faz esse tipo de avaliação, em 1987. Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), foram produzidos 757,51 milhões de dúzias no segundo trimestre deste ano, 5% a mais do que o registrado no mesmo período do ano passado. São Paulo foi o principal estado em produção de ovos de galinha em 2014, respondendo por 30,1% da produção nacional (IBGE, 2015). Considerado o segundo alimento mais completo, o ovo possui alto valor nutricional, é de fácil preparo, digestão e absorção, e fonte de nutrientes, principalmente de proteínas de alta qualidade (MURAKAMI et al., 2003).

---

Materiais e Métodos

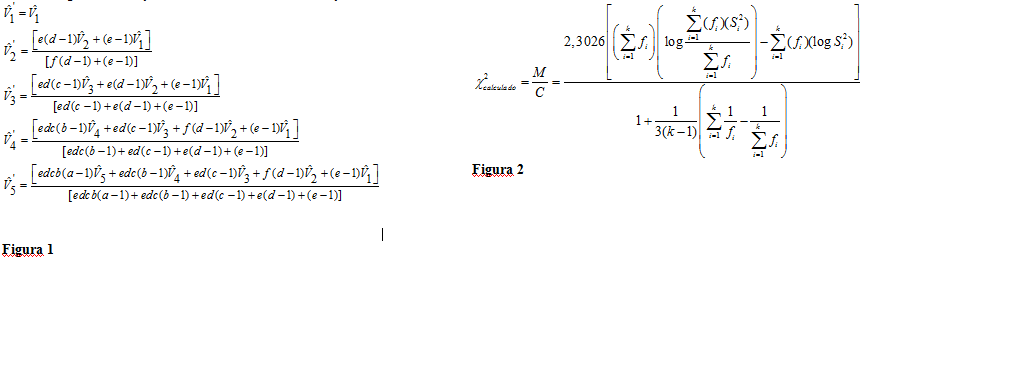
Os dados utilizados para a realização deste trabalho foram provenientes de 102 artigos com poedeiras comerciais, coletados nos sites de busca acadêmica,  no período de setembro de 2016 a janeiro de 2017. O instrumento computacional utilizado para analisar os dados foi o programa R (R DEVELOPMENT CORE TEAM, 2008). O Método da comparação de variâncias depende de um critério de classificação adotado para as análises de dados com o intuito de obter os tamanhos de parcela.  As estimativas das variâncias originais  para os tamanhos de parcelas obtidas por meio da análise de variância foram corrigidas em relação à menor unidade de classificação hierárquica, da seguinte forma: (figura 1) em que: i=1,...,5  considerando (5) tamanhos de parcelas obtidos através da classificação hierárquica,Vi, variância original das parcelas com X unidades básicas;Vi', variância corrigida; a, número de subsubparcelas em cada subparcela; b, número de subparcelas em cada parcela; c, número de parcelas em cada bloco; d, número de blocos em cada repetição; e, número de repetições. As estimativas das variâncias reduzidas V(Xi)  em relação a uma unidade básica foram obtidas dividindo-se as variâncias corrigidas V(Xi) , dos diferentes tamanhos de parcelas, pelos seus respectivos números de unidades básicas, como se segue: Vx=i = Sxi²/xi. Após estes procedimentos, aplicaram-se consecutivos testes de Bartlett para testar a homogeneidade das variâncias (Gomez & Gomez, 1984; Nunes, 1998), excluindo-se em cada teste, a menor parcela com variância significativamente diferente. Quando um grupo de parcelas de diferentes tamanhos com variâncias estatisticamente similares foi encontrado, o menor tamanho de parcela deste grupo que representou o tamanho ideal da unidade experimental. A estatística do teste é dada por: (figura 2) em que: X²calculado é a aproximação da distribuição Qui-quadrado com (k - 1) graus de liberdade e α representa o nível de significância, fi , número de graus de liberdade de cada estimativa de variância reduzida Vxi= Si² ; e , K número de estimativas.

---

Resultados e Discussão

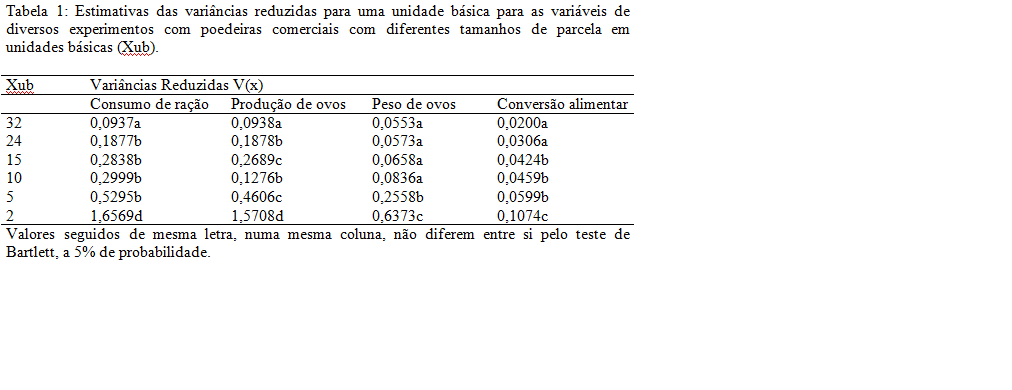
As hipóteses para testar homogeneidade das variâncias são: hipótese de nulidade H0: σ1² = σ2² = ... = σk²  e a hipótese alternativa Ha: pelo menos uma das variâncias diferem das demais. A conclusão do teste do qui-quadrado é, X²calculado ≥ X²(α,k-1), rejeita-se H0, caso contrário aceita-se H0. As variâncias reduzidas obtidas através de levantamento dos mais diversos experimentos com poedeiras comerciais para diferentes tamanhos de parcela em unidades básicas (Xub) para as diferentes variáveis obtidas foram estimadas e são apresentadas na Tabela 1. Aplicando-se consecutivos testes de homogeneidade de variâncias constatou-se que os tamanhos variando de 10 a 15 unidades básicas apresentaram variâncias estatisticamente iguais, exceto para produção de ovos, que foi inferior. Neste caso da igualdade das variâncias, considerou-se a parcela formada por 5 unidades básicas como sendo o melhor tamanho para as variáveis consumo de ração e conversão alimentar, 10 unidades básicas para peso de ovos e produção de ovos para as condições destes ensaios, uma vez que as variâncias não foram reduzidas significativamente quando parcelas maiores foram utilizadas.

---

Conclusões

Em experimentos com poedeiras comerciais o tamanho ótimo de parcela variou de 5 unidades básicas para as variáveis consumo de ração e conversão alimentar e 10 unidades básicas para peso de ovos e produção de ovos.

---

Gráficos e Tabelas

---

Referências

• IBGE, Instituto Brasileiro de Geografia e Estatística. Estatística da Produção Pecuária. 2015.
• LESSMAN, K.J.; ATKINS, R.E. Optimum plot size and relative efficiency of lattice designs for grain sorghum yield test. Crop Science, Madison, v.3, p.477-481, 1963.
• MEIER, V.D.; LESSMAN, K.J. Estimation of optimum field plot shape and size for testing yield in CrambeabyssinicaHochst. , Madison, v.11, p. 648-650, 1971.
• MURAKAMI, A. E.; FIGUEIREDO, D. F.; PERUZZI, A. Z. et al. Níveis de sódio para poedeiras comerciais no primeiro e segundo ciclos de produção. Ver. Bras. Zootec., Viçosa, v. 32, p. 1674-1680, 2003.
• R Development Core Team (2015). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org.
• STORCK, L. et al. Tamanho ótimo de parcela em experimentos com milho relacionado a metodologias. Revista Brasileira de Milho e Sorgo, v.5, 2006.
• SMITH, H. F. An empirical law describing heterogeneity in the yields of agricultural crops. Journal of Agricultural Science. Cambridge, v.28, p.1-23, jan.1938.
• USDA - International egg and poultry review, v.17, n.32, set. 2014.