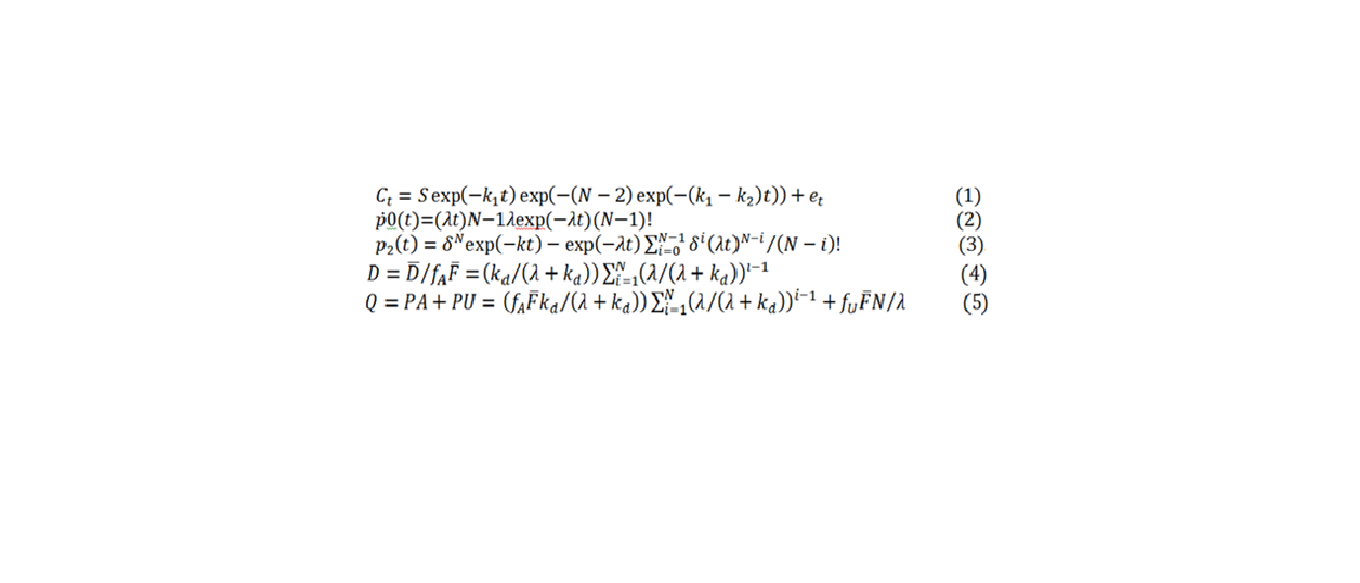Modelos não lineares para descrição do trânsito de partículas pelo trato digestório do ruminante: avaliação de modelos e implicações teóricas
2 - UENF
3 - UENF
4 - UENF
5 - UENF
6 - UENF
7 - UFV
8 - UENF
RESUMO -
Perfis fecais dos marcadores de partículas sólidas Cr e La, foram obtidos a partir de estudos cinéticos com vacas, novilhos e ovelhas, com o objetivo de avaliar modelos matemáticos utilizados para interpretar perfis de excreção de marcadores nas fezes. Os modelos MC, GN e o modelo GNG1 foram ajustados por meio do método de mínimos quadrados não lineares ordinários, avaliados com base nos critérios de probabilidade. Após o ajuste apresentaram diferenças em termos de probabilidade, no entanto, foram semelhantes em termos de aderência visual nos tempos observados; nas estimativas do tempo médio de retenção, houve sobreposição nos diferentes compartimentos. As principais diferenças numéricas observadas foram entre à média e a variância do tempo de trânsito para a primeira aparição do marcador nas fezes. O modelo que apresentou melhor ajuste foi o modelo GN, os modelos GNG1 e o Multicompartimental (MC) apresentaram equivalência em termos de probabilidade.
Nonlinear models to describe the transit of particles through the ruminant digestive tract: evaluation of models and theoretical implications
ABSTRACT - Fecal profiles of the particulate markers Cr and La, were obtained from digestion kinetic studies with cows, steers, and sheep with the aim of evaluating mathematical models designed to interpret marker excretion profiles in feces. The models evaluated were the model MC, the model GN, and the GNG1 model. Models were fitted with ordinary nonlinear least squares and evaluated on the basis of likelihood criteria. Despite remarkable differences in terms of likelihood, models were quite similar in terms of visual adherence to observed time profiles and presented overlapping interval estimates for compartment mean retention times. The major relative numerical discrepancies observed among models were related to the mean and variance of the transit time for the first appearance of the marker in feces. The model with best performance in mimicking the marker profiles were the GN model; the models GNG1 and Multicompartimental model (MC) were almost equivalent in terms of likelihood.Introdução
O rúmen é um sistema complexo e heterogêneo, formado por digesta líquida e sólida com estratificação deste conteúdo em diferentes camadas, o que torna o processo digestivo nos ruminantes um sistema dinâmico que envolve a entrada e saída de líquidos, microrganismos e resíduos não-digeridos. A modelagem matemática das funções produtivas, aliada à programação matemática e a avaliação empírica das predições com base nos resultados dos processos digestivos permite a compreensão deste complexo sistema e a formulação de dietas visando melhor desempenho dos animais. O objetivo do estudo foi a avaliação modelos matemáticos desenvolvidos para interpretar perfis de excreção dos marcadores nas fezes, os limites das inferências dos parâmetros e a compatibilidade dos pressupostos matemáticos e biológicos.Revisão Bibliográfica
Não é recente a preocupação na compreensão dos processos digestivos. Na literatura é possível observar uma continua busca pelo entendimento sobre o comportamento do fluxo da digesta e dinâmica de partículas no TGI dos ruminantes. Diversos autores empreenderam esforços na compreensão e na descrição dos processos ocorridos no TGI dos ruminantes domésticos (Ellis et al, 1979; 1984; Dhanoa et al. 1985; France et al. 1985). No entanto, devido ao arranjo peculiar do TGI e a heterogeneidade da digesta, estudos sobre cinética de partículas são complexos. Estudos pioneiros de modelagem por compartimentos foram conduzidos com o objetivo de traduzir a complexidade dos fenômenos naturais de forma que estes possam ser empregados na predição da realidade. Os conceitos estabelecidos nestes primeiros estudos têm sido aplicados com sucesso na nutrição de ruminantes, pois fornecem um referencial teórico sobre as transformações sofridas pela digesta no TGI (France et al., 1985; Matis, 1972; Waldo et al., 1972).Materiais e Métodos
Foram obtidos perfis fecais de marcadores de partículas sólidas de estudos com Cr, 52 perfis e La, 30 perfis (Vieira et al. (1997), e A. M. Fernandes (resultados não publicados). As espécies domésticas de ruminantes utilizadas foram bovinos e ovinos; Novilhos (perfis de 12 Cr) e vacas secas (6 perfis de Cr) e vacas leiteiras em lactação (28 perfis Cr) formaram o grupo de bovinos. O grupo de ovinos contribuiu com 6 perfis de Cr, 30 La. Os modelos (MC) eq. (1), GN (2) e GNG1 (3) foram ajustados para interpretação dos dados. Na equação (1) Ct é a concentração do indicador (mg/kg) de partícula nas fezes no tempo t(h), ???????? é o erro aleatório, ???? parâmetro escalar em função de ????1, ????2 e ????. A equação (2) representa uma expansão do modelo proposto por Blaxter et al. (1956), em que foram introduzidos elementos estocásticos no modelo. Em que ????̇0(????) é a função densidade de probabilidade associada a ????, ???? é o valor assintótico da taxa de passagem fracionária tempo dependente para N > 1, N é um inteiro positivo, cujos valores são válidos para N≥2. O modelo GNG1 ajustado conforme a equação (3) e apresenta formulação geral baseada no tempo retenção como variável aleatória, com um tempo fixo de atraso (t) e um tempo total de permanência da partícula no sistema. Os modelos foram ajustados por meio do PORC NLIN do SAS, o algoritmo utilizado para minimização da soma do quadrado dos erros foi o método de Newton. Entretanto quando a correlação entre os parâmetros foi maior que 0.9 o algoritmo escolhido foi o de Marquardt. A qualidade do ajuste foi avaliada por meio da corrida de sinais do resíduo e pelo critério de verossimilhança. Os modelos foram ranqueados com base no critério de informação de Akaike corrigido (AICch), as diferenças, Δ=AICch-minimumAICch, a probalidade de verossimilhança (Wh) e a razão de evidência para cada um dos modelos foram descritas de acordo as recomendações de Burnham e Anderson (2004) e Vieira et al. (2012).Resultados e Discussão
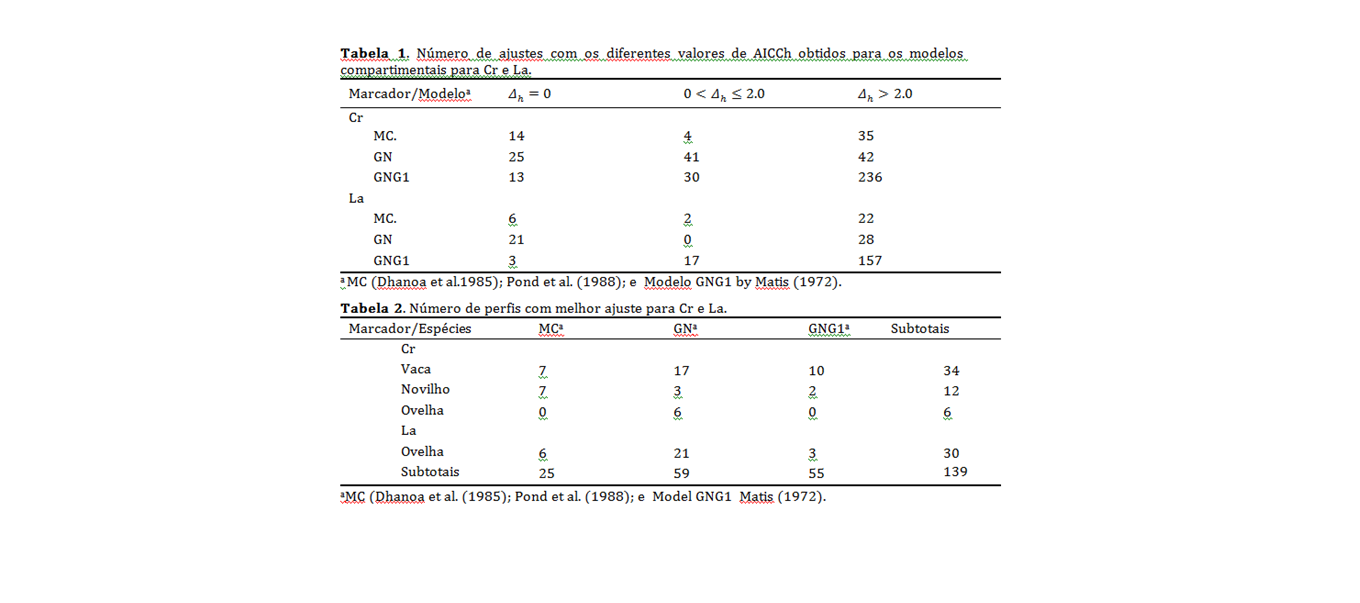
O número de ajustes com Δh=0 revela uma superioridade do modelo GN em relação aos demais em simular os perfis de marcadores de partículas sólidas Cr e La Tabela (1). O modelo MC descrito na eq.(1) apresentou ajuste semelhante ao modelo GNG1 para Cr e La, se considerarmos apenas os melhores ajustes Δh=0. Em geral o modelo GN tem maior probabilidade de simular os perfis de Cr e La. Esta condição pode ser explicada, pois o N do modelo GN variou de 2 a 6, o N do modelo GNG1 variou de 1 a 6, o número de modelos ou de hipoteses equivalentes para os modelos foi de 12 para cada um dos marcadores testados. Utilizando alguns critérios adicionais para seleção do melhor modelo, i.e, 0 ≤ Δh ≤ 2.0; t ≥ 7.0, observamos que os melhores ajustes para os perfis de excreção dos indicadores de particulas sólidas, foram obtidos com o modelo GN, seguido do modelo GNG1 e do MC tabela (2). O critério de Akaike e suas medidas derivadas são excelentes avaliadores da qualidade do ajuste do modelo como evidenciado nas figuras 1 e 2. A razão de evidência apresentou valores elevados em algumas situações, demonstrando que os modelos com estas características não apresentam capacidade de simular a excreção dos marcadores. Como se observa que no modelo GNG1 para N=1 apresenta Δh=0.0 e Wh=0.891 e o modelo MC Δh=14.7 e Wh=0.001, no entanto, a diferença visual é praticamente nula. Nesta condição o GNG1 apresenta aos seguintes resultados μ ̂t=τ ̂+1⁄λ ̂ +1⁄k ̂ =34.8 e σ ̂t=17.3 e o MC μ ̂t=35.9 e σ ̂t=18.7e por razões práticas o pode ser predito pelos dois modelos. A retenção de partículas no TGI de ruminantes tem sido investigada com intuito de avaliar a qualidade dos substratos digeridos no rúmen e no reticulo e no restante do trato digestório. Com essa informação, é possível estimar as quantidades de energia e proteína metabolizáveis disponíveis para a mantença e produção a partir de proteínas digeridas, carboidratos e frações lipídicas. A quantidade de substrato é resultado de processos competitivos de digestão e escape ao longo do TGI. Os modelos utilizados no presente estudo não apresentaram, pelo menos visualmente, diferenças em termos de aderência aos perfis de excreção. Os perfis, calculados por France et al. (1985) e Matis et al. (1989), apresentaram tempo de retenção médio total com sobreposição de intervalos. No entanto, as diferenças de probabilidade entre os modelos a variabilidade das estimativas para τ foram notáveis. Para os casos em que o modelos GN foi escolhido como melhor ajuste, foi necessária a dedução de modelo para explicar a digestibilidade e o preenchimento ruminoreticular, para interpretação dos perfis de excreção dos marcadores conforme equações (4) e (5).Conclusões
O modelo com a melhor capacidade de ajuste aos perfis dos marcadores foi o modelo de GN; o modelo de GNG1 e o modelo MC foram praticamente equivalentes em termos de probabilidade. Fica circunscrito que as diferenças entre os três modelos estudados são conceituais. Devido a este fato, foi proposta uma modelagem alternativa, para os casos em que o modelo GN for melhor ajuste que os modelos GNG1 e eq. (1).Gráficos e Tabelas