ESTIMATIVA DA CURVA CRESCIMENTO DE CAPRINOS DE RAÇAS LEITEIRAS UTILIZANDO MODELOS NÃO LINEARES COMBINADOS À DIFERENTES ESTRUTURAS DE VARIÂNCIA
Carlos Henrique Paiva Camisa Nova1, Norberto da Silva Rocha2, Matheus Lima Corrêa Abreu3, Davi Leal Barbosa4, Antônio Paulo Oliveira Neto5, Daniel Furtado Dardengo Sant Anna6, Kamila da Silva Alvarenga7, Leonardo Siqueira Glória8
1 - Universidade Estadual do Norte Fluminense - Darcy Ribeiro
2 - Universidade Federal dos Vales do Jequitinhonha e Mucuri
3 - Universidade Federal de Minas Gerais
4 - Universidade Estadual do Norte Fluminense - Darcy Ribeiro
5 - Universidade Estadual do Norte Fluminense - Darcy Ribeiro
6 - Universidade Estadual do Norte Fluminense - Darcy Ribeiro
8 - Universidade Estadual do Norte Fluminense - Darcy Ribeiro
2 - Universidade Federal dos Vales do Jequitinhonha e Mucuri
3 - Universidade Federal de Minas Gerais
4 - Universidade Estadual do Norte Fluminense - Darcy Ribeiro
5 - Universidade Estadual do Norte Fluminense - Darcy Ribeiro
6 - Universidade Estadual do Norte Fluminense - Darcy Ribeiro
8 - Universidade Estadual do Norte Fluminense - Darcy Ribeiro
RESUMO -
A estimativa da curva de crescimento de caprinos por meio de modelos matemáticos pode ser uma ferramenta base para traçar estratégias em sistemas de produção. Assim, o objetivo do presente trabalho foi avaliar o perfil de crescimento em caprinos leiteiros utilizando modelos matemáticos. Foram realizados abates de 32 cabritos machos castrados das raças Saanen e Pardo Alpina. Os animais foram abatidos com 0, 15, 90, 135, 210, 270, 365 e 485 dias de vida, sendo 4 animais abatidos para cada idade. As variáveis foram avaliadas quanto a verossimilhança à quatro modelos não lineares previamente selecionados (Brody, Logístico, Gompertz e Richards) com 4 estruturas de variância (Homogêneo, Heterogêneo, Exponencial e Assintótico). O modelo que apresentou maior verossimilhança para a maioria das variáveis foi o modelo de Gompertz com a estrutura de variância exponencial. O modelo de Gompertz apresenta maior verossimilhança para a maioria das variáveis até a idade de 485 dias de vida de caprinos de raças leiteiras.
Palavras-chave: modelagem, pecuária, pequenos ruminantes
GROWTH PROFILE EVALUTION OF DAIRY GOATS BY NONLINEAR MODELS COMBINED TO DIFFERENT VARIANCES
ABSTRACT - The evaluation of the growth curve in goats for mathematical models may be useful to decide strategies in goat production systems. Thus, the goal in this study was to evaluate growth profile of dairy goats using mathematical models. 32 castrate male from breeds Saanen and alpine were slaughtered. The animals were slaughtered at 0, 15, 90, 135, 210, 270, 365, 485 days, four animals at each age. The variables were evaluated by likelihood through 4 nonlinear models previously selected (Brody, Logistico, Gompertz and Richards) with four variances (Homogeneous, Heterogeneous, Exponential and Asymptotic). The model that presented greater likelihood to the most of the variables was Gompetz-exponential. The Gompertz model was the greater likelihood to the most of variables until 485 days of life for dairy goats.Keywords: modeling, livestock, small ruminants
Introdução
O mecanismo de crescimento animal pode ser entendido como um fenômeno complexo, o qual apresenta grande importância para a Zootecnia. O entendimento sobre o comportamento de crescimento pode promover a intensificação da produção pecuária, uma vez que permite relacionar as faixas de peso e idade ideais dos animais para serem submetidos, por exemplo, à reprodução ou ao abate. As relações matemáticas entre massa corporal e idade caracterizam o estudo das curvas de crescimento. A curva de crescimento apresenta forma sigmoide em boa parte dos casos, com uma fase de aceleração da taxa de crescimento nas idades iniciais, um ponto de inflexão (máxima taxa de crescimento) e uma fase de desaceleração da taxa de crescimento até que a assíntota seja alcançada (Brody,1945). A matemática tem sido cada vez mais empregada nos sistemas pecuários como ferramenta importante para auxiliar nos processos decisórios, possibilitar a simulação de cenários e antecipar a repercussão de diferentes cursos de ação sobre os sistemas reais de produção. Desta forma, objetivou-se avaliar quantitativamente o processo de crescimento em caprinos por meio de ajuste de modelos matemáticos a perfis de crescimento de machos castrados de raças leiteiras.Revisão Bibliográfica
O crescimento animal é resultado líquido positivo entre os processos catabólicos e anabólicos (BERTALANFFY, 1957), o qual é influenciado pelo potencial genético do indivíduo e pelas condições ambientais às quais é submetido (BRODY, 1945). Em termos práticos, o crescimento animal pode ser entendido como um processo morfofisiológico que tem início ainda na fase pré-natal e termina quando o organismo atinge o peso, a maturidade e a conformação característica da espécie. A modelagem matemática pode ser entendida como uma ferramenta útil, adotada para auxiliar o processo decisório, por meio da simulação de cenários e predição de diferentes cursos de ação de um sistema específico (DIAS, 1996; BARIONI, 2002). Adicionalmente, a adoção de modelos matemáticos permite descrever e compreender alguns dos processos que ocorrem no interior do sistema e as interações entre seus componentes (BELLOTI, 2000; BARRET e NEARING, 1998). Os modelos matemáticos são formulações matemáticas que tentam representar fenômenos físicos ou sistemas biológicos, com a finalidade de gerar uma equação que possa representar fenômeno (s) a um determinado nível de verossimilhança. As curvas de crescimento animal podem ser caracterizadas como representações gráficas das relações matemáticas existentes entre o acúmulo de massa corporal (M) em função do tempo (t). (FITZHUGH, 1976; GOTTSCHALL, 1999). Modelos matemáticos algébricos simples têm sido aplicados para auxiliar o planejamento pecuário da atividade zootécnica. Contudo, tem sido intensificada a adoção de modelos matemáticos mais complexos no sistema de produção animal, nos quais são admitidas abordagens não lineares para descrever, por exemplo, os estudos referentes ao crescimento animal, curvas de lactação, cinética de digestão e demais particularidades (FRANCE et al., 1996; TEDESCHI et al., 2005; VIEIRA et al., 2005). Entre as aplicações dos conceitos que envolvem o estudo das curvas de crescimento na produção animal, podem ser destacados: resumir as características de crescimento da população em três ou quatro parâmetros; avaliar o perfil de respostas de tratamentos ao longo do tempo; estudar as interações de respostas das subpopulações ou tratamentos com o tempo e obter a variância entre e dentro de indivíduos de grande interesse nos programas de melhoramento genéticos (FREITAS, 2005).Materiais e Métodos
Neste estudo, 32 animais foram utilizados para gerar os perfis de crescimento. Os animais foram abatidos em idades pé estabelecidas, são elas: 0, 15, 90, 135, 210, 270, 365, 485 dias de vida. Em cada idade de abate, 4 animais eram escolhidos aleatoriamente para serem, devidamente, eviscerados e pesados para se obter as variáveis peso corporal (W), peso corporal vazio (EBW), carcaça (carcass), vísceras (organs) e trato gastrointestinal (GIT). O peso corporal foi obtido com a pesagem do animal vivo. A variável EBW foi obtida através da pesagem da carcaça, sangue, cabeça, couro, patas, cauda, órgãos, gordura renal-pélvica-inguinal e vísceras vazias e limpas. A carcaça foi devidamente separada em duas e foi retirado o excesso de gordura das mesmas e, finalmente, pesadas juntas. As vísceras foram pesadas conjuntamente, sendo elas: coração, pulmões, traqueia, fígado e vesícula biliar, baço, rins, língua com faringe e laringe, esôfago, trato reprodutivo e bexiga. O trato gastrointestinal foi pesado completo após a remoção do conteúdo residual contido em cada segmento do GIT. Após o término do abate dos animais nas suas respectivas idades pré-estabelecidas e, com suas variáveis obtidas, cinco modelos de crescimento foram selecionados para avaliar a verossimilhança com os perfis de crescimento gerados pelas variáveis, são eles: Monomolecular (Brody, 1945), Logístico, Gompertz, Richards e Michaelis-Menten Generalizado (France et al., 1996; López et al., 2000), sendo todos testados com quatro estrutura de variância, que são: Homogênea (hg), Heterogênea discreta, Exponencial (exp) e Assintótica (asy). Os modelos foram ajustados com uso do procedimento NLMIXED do SAS (version 9, SAS System Inc., Cary, NC, USA), sendo o principal critério a validar o modelo o qual apresentar a maior probabilidade de verossimilhança.Resultados e Discussão
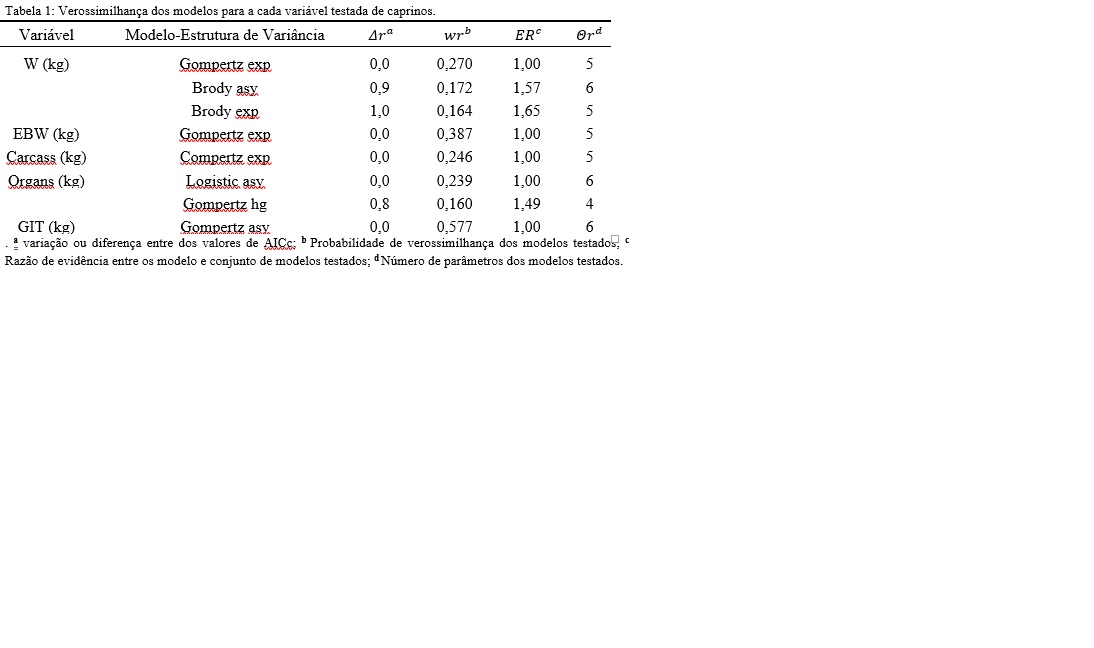
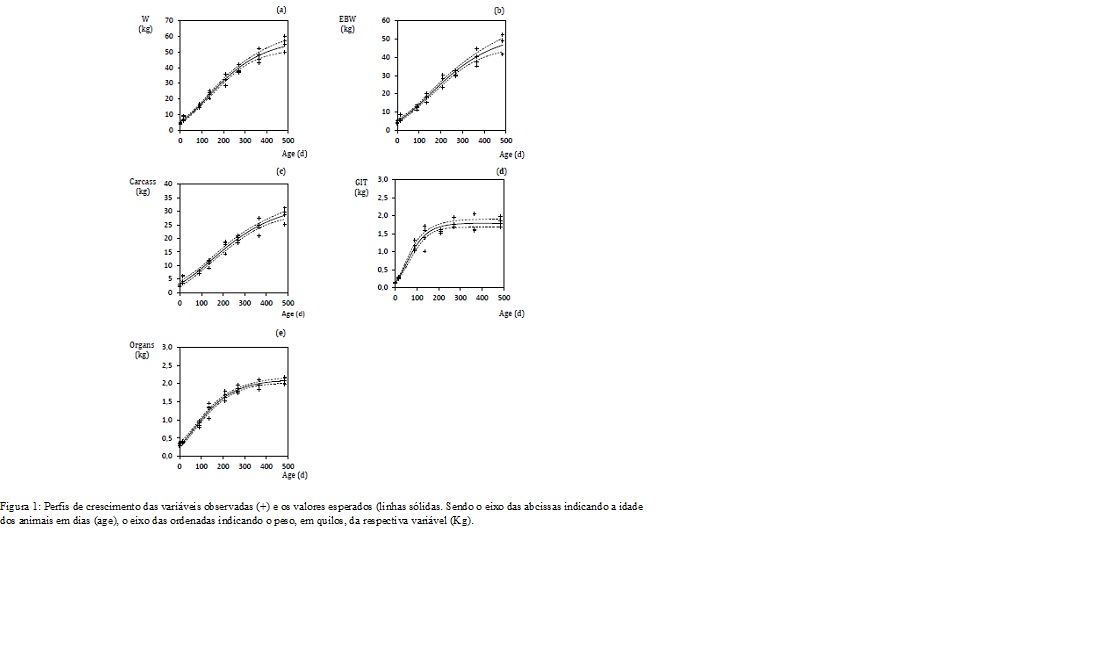
Para a maioria das variáveis, o modelo de Gompertz apresentou maior verossimilhança (80%) e a estrutura de variância exponencial foi a melhor em 60% dos casos (Tabela 1). O padrão de crescimento de algumas variáveis dos conjuntos experimentais, W, EBW e carcaça, não apresentou um comportamento assintótico. O modelo de Gompertz não tem um parâmetro explícito representando a assíntota alcançada pelo crescimento final (Thornley and France, 2005). Os perfis de crescimento para cada uma das variáveis peso corporal, peso corporal vazio, peso de carcaça, peso de vísceras e peso do trato gastrointestinal foram esboçados para avaliar o comportamento da curva (figura 1abcde).Conclusões
O modelo de Gompertz apresenta maior verossimilhança para a maioria das variáveis até a idade de 485 dias de vida de caprinos de raças leiteiras.Gráficos e Tabelas
