Modelagem matemática como ferramenta de predição de crescimento do Piaractus mesopotamicus em sistema de produção semi-intensivo
Guilherme Wolff Bueno1, Maicon da Rocha Brande2, Antônio Fernando Leonardo3, Érica Machado Fernandes4, Rafael V. Reis Neto5, Érico Tadao Teramoto6, Luis Carlos Ferreira de Almeida7
1 - Universidade Estadual Paulista “Júlio Mesquita Filho” – Unesp, Campus Experimental de Registro, Curso de Engenharia de Pesca.
2 - Universidade Estadual Paulista “Júlio Mesquita Filho” – Unesp, Campus Experimental de Registro, Curso de Engenharia de Pesca.
3 - Agência Paulista de Tecnologia dos Agronegócios – APTA, Polo Regional de Desenvolvimento Tecnológico do Agronegócio do Vale do Ribeira
4 - Centro de Aquicultura da Universidade Estadual Paulista “Júlio de Mesquita Filho” – CA/Unesp, Campus de Jaboticabal, Mestrado em Aquicultura.
5 - Universidade Estadual Paulista “Júlio Mesquita Filho” – Unesp, Campus Experimental de Registro, Curso de Engenharia de Pesca.
6 - Universidade Estadual Paulista “Júlio Mesquita Filho” – Unesp, Campus Experimental de Registro, Curso de Engenharia de Pesca.
7 - Universidade Estadual Paulista “Júlio Mesquita Filho” – Unesp, Campus Experimental de Registro, Curso de Engenharia de Pesca.
2 - Universidade Estadual Paulista “Júlio Mesquita Filho” – Unesp, Campus Experimental de Registro, Curso de Engenharia de Pesca.
3 - Agência Paulista de Tecnologia dos Agronegócios – APTA, Polo Regional de Desenvolvimento Tecnológico do Agronegócio do Vale do Ribeira
4 - Centro de Aquicultura da Universidade Estadual Paulista “Júlio de Mesquita Filho” – CA/Unesp, Campus de Jaboticabal, Mestrado em Aquicultura.
5 - Universidade Estadual Paulista “Júlio Mesquita Filho” – Unesp, Campus Experimental de Registro, Curso de Engenharia de Pesca.
6 - Universidade Estadual Paulista “Júlio Mesquita Filho” – Unesp, Campus Experimental de Registro, Curso de Engenharia de Pesca.
7 - Universidade Estadual Paulista “Júlio Mesquita Filho” – Unesp, Campus Experimental de Registro, Curso de Engenharia de Pesca.
RESUMO -
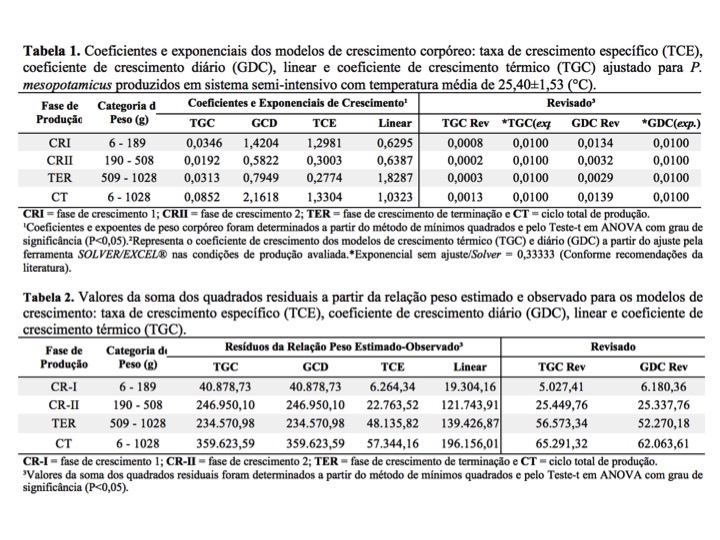
O objetivo deste estudo foi avaliar modelos de predição corporal para definição dos exponenciais de crescimento do pacu (Piaractus mesopotamicus) produzidos em viveiros escavados em sistemas semi-intensivo na região do Vale do Ribeira no estado de São Paulo. Realizou-se o acompanhamento dos ciclos de produção do pacu, em cinco pisciculturas durante dois anos, estes foram divididos em 3 fases de peso (05 a 200g = CRI; 200 a 510g = CRII e 510 a 1kg = TER) e ciclo total (05 a 1kg = CT). Utilizaram-se os modelos matemáticos TGC, GDC, TCE e Linear para predição do crescimento corporal e definição dos exponenciais de crescimento (exp.) para cada fase de cultivo. Verificaram-se que o modelo TGC nas fases CRI, CRII e TER valores de exp. de 0,0346; 0,0192 e 0,0313, respectivamente. Os modelos GDC, TCE e Linear apresentaram exp. médio de 0,3333 para as fases CRI, CRII, TER e CT. O TGC e GDC apresentam a melhor precisão para modelagem do peso corporal do P. mesopotamicus neste sistema de cultivo.
Palavras-chave: aquicultura de precisão, curvas de crescimento, modelagem matemática, pacu.
Mathematical modeling as a tool to predict the growth of Piaractus mesopotamicus in a semi-intensive production system
ABSTRACT - The objective of this study was to evaluate body prediction models for the definition of growth exponents of pacu (Piaractus mesopotamicus) produced in nurseries excavated in semi-intensive systems in the Ribeira Valley region located in São Paulo State. During two years, ten cycles of pacu production were monitored in five fish farms, which were divided into three weight stages (05 to 200g = CRI, 200 to 510g = CRII and 510 to 1kg = TER) and total cycle (05 to 1kg = CT). Four mathematical models (TGC, GDC, TCE and Linear) were used for predict body growth and to define growth exponentials (exp.) It was verified that the TGC model in the CRI, CRII and TER phases presents exp. of 0.03460, 0.01929 and 0.03133, respectively. The GDC, TCE and Linear models presented exp. 0.3333 for the CRI, CRII, TER and CT phases. The TGC and GDC models present results with better precision of growth of Piaractus mesopotamicus in a semi-intensive production system.Keywords: aquaculture, fish growth, pacu, growth body, factorial model.
Introdução
A aquicultura (produção de organismos aquáticos) é uma alternativa para incrementar os índices de consumo de proteínas de origem animal e um importante fator de desenvolvimento socioeconômico para o país (FAO, 2016). Dentre as espécies de peixes produzidas no país, ressaltam-se a produção de espécies nativas como o pacu (Piaractus mesopotamicus) com crescimento de 6,6% no ano de 2014 (IBGE, 2014). Este aumento, deve-se a adaptação destas espécies aos diversos sistemas de produção, características como rusticidade, elevado rendimento de carcaça, evolução nas tecnologias de reprodução e uso de rações específicas (KLEIN et al., 2014). Diante disto, a determinação e análise do potencial de crescimento corporal por meio da modelagem matemática pode auxiliar o planejamento e manejo das operações aquícolas nas pisciculturas (BUENO, 2015). Neste cenário, o uso de modelos matemáticos de predição corporal tem-se tornado o modo mais eficiente para maximizar e avaliar o crescimento animal, além de permitir a definição do peso final do animal em um determinado tempo para comercialização (DUMAS et al., 2010). Portanto, o objetivo deste estudo consista na aplicação de modelos matemáticos de predição corporal para definição de exponenciais de crescimento para o Piaractus mesopotamicus produzidos em viveiros escavados em sistemas semi-intensivo na região do Vale do Ribeira no estado de São Paulo.Revisão Bibliográfica
A maneira mais propícia para maximizar a eficiência e melhorar o crescimento animal pode ser realizada por meio do uso de modelos matemáticos que predizem as taxas de crescimento e os requisitos alimentares dos peixes. Estes modelos podem, se utilizados corretamente, tornar-se uma ferramenta muito útil, tanto para o planejamento da produção, do ponto de vista da gestão, quanto no auxílio de estratégias futuras, ao compararmos o estado atual do cultivo com o que poderia ser obtido de forma viável biologicamente em um cenário posterior (Iwama e Tautz, 1981; Cho e Bureau., 1998; Bureau et al., 2002). Neste contexto, o uso de tecnologias e ferramenta que melhorem a precisão e eficiência nas operações aquícolas tem se tornado a principal aliada dos piscicultores em busca de resultado e minimização de risco durante a produção. Dentre estas necessidades está a substituição de biometrias e manejo para avaliar o crescimento corporal por meio do uso de modelagem matemática. Iwama e Tautz (1981) ressaltam que apesar de muitas tentativas de desenvolver expressões matemática para descrever o crescimento dos peixes, existe uma grande diversidade de abordagens e conceitos. Neste cenário, é comum encontrarmos o crescimento expresso em centímetro por mês, taxas de crescimento instantâneas, porcentagem de mudança de comprimento ou a porcentagem de mudança no peso, muitas vezes sem qualquer referência a temperaturas, alimentação ou condições de cultivo (NRC, 2013). Portanto, um modelo de crescimento adequado permitirá estimativas dos requisitos (de alimentação) da energia do peixe e de suas taxas de crescimento. Esta informação permitirá ao produtor a resolução de vários problemas relacionados ao crescimento e taxa de alimentação que surgem na rotina de uma fazenda (Dumas et al., 2010).Materiais e Métodos
O estudo foi realizado durante dois anos, de 2014 a 2015 no Campus experimental de Registro da Universidade Estadual Paulista – UNESP por meio da coleta de dados em cinco pisciculturas comerciais instaladas na região do Vale do Ribeira, região sudoeste do estado de São Paulo. Realizaram-se a identificação e triagem das unidades amostrais (propriedades produtoras de P. mesopotamicus). Mensalmente avaliou o peso corporal individual de 10% da biomassa de cada viveiro, além de medições diárias da temperatura da água (oC) durante todo ciclo de produção. Classificaram-se as fases de produção de acordo com a categoria de peso observada (05 a 200g = CRI; 200 a 510g = CRII e 510 a 1kg = TER) e ciclo total (05 a 1kg = CT). Aplicou-se a modelagem matemática de predição corporal por meio das equações de crescimento Linear (Eq. 1), Taxa de Crescimento Específico (TCE) (Eq. 2), Coeficiente de Crescimento Diário (GDC) (Eq. 3) e Coeficiente de Crescimento Térmico (TGC) (Eq. 4), no qual o expoente de peso corporal foi mantido fixo (1-b = 0,33333). Em seguida, o peso final (Pf) foi calculado por meio da reorganização das equações de 1 a 4 para os respectivos modelos: Eq. (1): Pf (g) = [Intercepto + (Vértice x Pi) ]; Eq. (2): Pf (g) = xp { [ln(Pi) ] + [ (TCE x (df – di) / 100) ] }; Eq. (3): Pf (g) = {Pi (1/3) + [ (DGC x (df - di) / 100) ] }3; Eq. (4): Pf (g) = {Pi (1-b) + [ (TGC x Σt x (df – di) / 100) ] }1 / (1-b) Onde: Pi e Pf é o peso inicial e final corporal, respectivamente, d é dia, t é temperatura (°C), e (1-b) é o expoente do peso corporal (DUMAS et al., 2010). A partir dos valores de crescimento obtidos por estes modelos, aplicou-se a técnica de mínimos quadrados (SOMAQUAD/Microsoft Office Excel®) para minimizar a soma dos quadrados dos resíduos (RSS). O ajuste das curvas de crescimento foi elaborado a fim de gerar o melhor exponencial de crescimento para P. mesopotamicus pelo método de interação.Resultados e Discussão
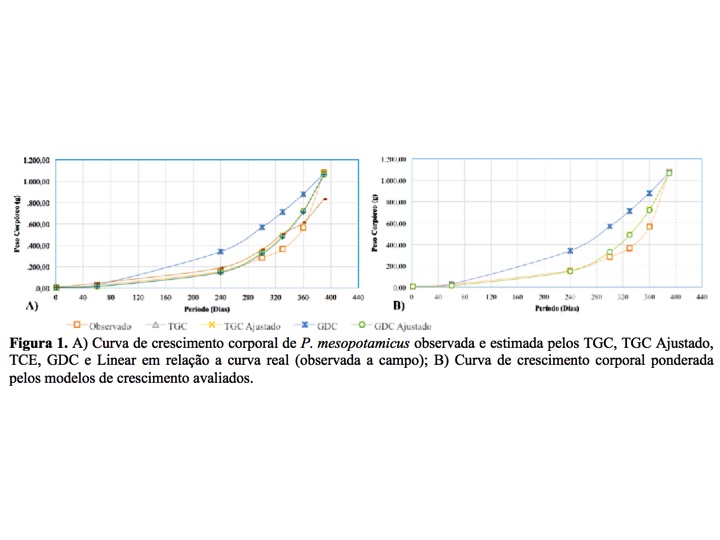
Observaram-se na Tabela 1 as diferenças para cada fase de produção em relação ao coeficiente de crescimento. A mesma relação pode ser observada para os modelos GDC, TCE e Linear, para as fases CRI, CRII, TER e CT, dos quais os valores apresentam como exponencial de variação valor igual a 0,3333 anterior a avaliação e ajuste residual (Tabela 2). Dentre os modelos matemáticos avaliados, os modelos Linear e TCE apresentaram menor precisão quando comparado ao peso real (observado a campo), em função da ponderação dos exponenciais de crescimento (Figura 01). Segundo Iwama & Tautz (1981) este modelo matemático é pouco preciso por desconsiderar oscilações e diferenças de crescimento em relação a temperatura da água durante o período de avaliação. Caso semelhante foi observado no modelo TCE, onde o coeficiente é inferior aos demais modelos matemáticos, e ainda por ser uma equação logaritimizada, o logaritmo natural não corresponde ao padrão da curva de crescimento em relação a curva real observada para a espécie, fato também verificado para Oncorhynchus mykiss, Salmo salar e Oreochromis niloticus (IWAMA & TAUTZ, 1981; BUREAU et al., 2006; DUMAS et al., 2010). Após a realização do ajuste dos exponenciais de crescimento pela ferramenta SOLVER/Excel® na Tabela 1, observam-se valores precisos para coeficientes de crescimento quando calculado o peso estimado em relação ao peso real (observado a campo), tanto para o modelo de crescimento TGC, quanto para o modelo GDC, à um exponencial de crescimento igual a 0,01. Dos quais, refletem nos valores de soma dos quadrados residuais (Tabela 2), apresentando valores menores em relação aos coeficientes sem o ajuste pela ferramenta SOLVER/Excel®. No entanto. Na Figura 1, apresentam-se as curvas de crescimento dos modelos ajustados de TGC e GDC, para efeito de comparação com o crescimento observado no campo. Segundo Dumas et al. (2010) o ajuste das curvas de crescimento conforme o elaborado por este presente estudo, permite gerar um melhor exponencial de crescimento para as espécies, devido as interações matemáticas e o efeito da redução da soma dos quadrados de resíduos. Corroborando com o observado por Bueno et al. (2015) na avaliação da produção comercial de O. niloticus em um reservatório tropical. Na Figura 1-B, apresentam-se as curvas de crescimento corpóreo de P. mesopotamicus dos modelos matemáticos TGC e TGC Ajustado em relação ao peso observado a campo, a partir da ponderação do efeito da temperatura durante todo ciclo de produção. Observa-se uma variação da temperatura durante o período de produção em torno de 21°C a 31,6°C, cuja temperatura média ficou na casa dos 25,4 °C a qual pode ser ajustada de acordo com o exp. obtido. Com isso, a parir do uso da modelagem matemática pode-se definir a temperatura exata em que o indivíduo expressará todo seu potencial zootécnico (BUENO, 2015), e com isso tornar o sistema de produção mais eficiente (BUREAU et al., 2006; DUMAS et al., 2010).Conclusões
Os modelos matemáticos de coeficiente térmico de crescimento (TGC) e coeficiente de crescimento diário (GDC) com exponenciais ajustados, apresentam a melhor precisão para predição corporal do Piaractus mesopotamicus produzidos em viveiros escavados em sistemas semi-intensivo.Gráficos e Tabelas
