Modelos matemáticos (Gompertz e Von Bertalanffy) para determinar o crescimento de três linhagens de frangos caipira
Kênia Ferreira Rodrigues1, Roberta Gomes Marçal Vieira Vaz2, Caroliny Costa Araújo3, Carla Fonseca Alves Campos4, Aline Ferreira Amorim5, Valquíria Sousa Silva6, Luciano de Almeida dos Santos7, Mara Regina Ribeiro Cardoso8
1 - Universidade Federal do Tocantins
2 - Universidade Federal do Tocantins
3 - Universidade Federal do Tocantins
4 - Universidade Federal do Tocantins
5 - Universidade Federal do Tocantins
6 - Universidade Federal do Tocantins
7 - Universidade Federal do Tocantins
8 - Universidade Federal do Tocantins
2 - Universidade Federal do Tocantins
3 - Universidade Federal do Tocantins
4 - Universidade Federal do Tocantins
5 - Universidade Federal do Tocantins
6 - Universidade Federal do Tocantins
7 - Universidade Federal do Tocantins
8 - Universidade Federal do Tocantins
RESUMO -
Objetivou-se com este trabalho identificar, por meio de diferentes critérios estatísticos, o ajuste do modelo de regressão não linear mais adequado para descrever a curva de crescimento de três linhagens de frangos de corte do tipo caipira. Utilizou-se 90 aves caipiras, sendo 30 aves de cada uma das seguintes linhagens: Pescoço Pelado, Carijó e Pesadão Vermelho. Foi coletado semanalmente o peso corporal individual dos frangos para determinação das curvas de crescimento por meio dos modelos Von Bertalanffy e Gompertz. Entre os modelos utilizados, Gompertz mostrou-se mais adequado, devido menor índice assintótico evidenciando o modelo de melhor ajuste.
Palavras-chave: idade, linhagens, modelos estatísticos
Mathematical models (Gompertz and Von Bertalanffy) to determine the growth of three lineages chickens caipira
ABSTRACT - The objective of this work was to identify, by means of different statistical criteria, the adjustment of the nonlinear regression model that is most adequate to describe the growth curve of three slow growing chickens lineages. A total of 90 birds were used, with 30 birds from each of the following lineages: Pescoço Pelado, Carijó and Pesadão Vermelho. The individual body weight of the chickens was collected weekly to determine the growth curves using the Von Bertalanffy and Gompertz models. Among the models used, Gompertz was more adequate, due to the lower asymptotic index evidencing the best fit modelKeywords: age, lineages, statistical models
Introdução
A criação de frangos tipo caipira, ou aves de crescimento lento, é um dos segmentos da avicultura alternativa que tem se mostrado promissor, pois, além de agregar valor ao produto e utilizar um sistema de criação que preza pelas normas de bem-estar animal (MORAIS et al, 2015). Sabe-se que o desenvolvimento do frango tipo caipira até o ponto de abate leva maior tempo que frangos de corte comercial. Sendo assim, o conhecimento da curva de crescimento pode auxiliar na escolha a adoção de práticas de manejo que otimizem a produção de carne, priorizando as necessidades nutricionais de cada fase de crescimento, estabelecendo programas alimentares específicos, com definição da idade ótima de abate (BRACCINI NETO, 1993). Desse modo, objetivou-se identificar, por meio de diferentes modelos matemáticos, o ajuste do modelo de regressão não linear mais adequado para descrever a curva de crescimento de três linhagens de frangos de crescimento lento.Revisão Bibliográfica
Até a década de 60, os animais criados não possuíam padrão de raça definido, sem controle quanto aos cruzamentos. A partir de então, o melhoramento genético por meio dos avanços tecnológicos busca desenvolver aves de linhagens e raças melhoradas geneticamente, visando obter animais resistentes e produtivos (KISHIBE et al., 1998). Os animais utilizados devem apresentar as seguintes características: alta rusticidade, adaptabilidade e potencial genético inferior para o crescimento (CAIRES; CARVALHO; CAIRES, 2010). Algumas linhagens são disponíveis no mercado por instituições e empresas privadas ou associações, que devem ser regulamentadas para atestar a idoneidade de seus produtos. O biótipo animal é definido pelo peso associado a maturidade sexual em relação ao tamanho esquelético, demonstrado pelo comprimento do corpo e altura em função da idade (MOTA et. al, 2014). A velocidade que o animal cresce irá depender da espécie que pertence. Animais de porte pequeno apresentam crescimento mais rápido, com taxa inicial de crescimento elevada, um período curto de crescimento, atingindo assim a maturidade mais cedo em relação aos de grande porte. O sexo do animal também influencia seu crescimento, pois o macho é mais pesado e a fêmea mais leve, sendo que fêmea tem velocidade inicial de crescimento e peso adulto final menor (THOLON; QUEIROZ, 2009). Sendo assim, o conhecimento da curva de crescimento pode auxiliar na escolha a adoção de práticas de manejo que otimizem a produção de carne, priorizando as necessidades nutricionais de cada fase de crescimento, estabelecendo programas alimentares específicos, com definição da idade ótima de abate (BRACCINI NETO, 1993).Materiais e Métodos
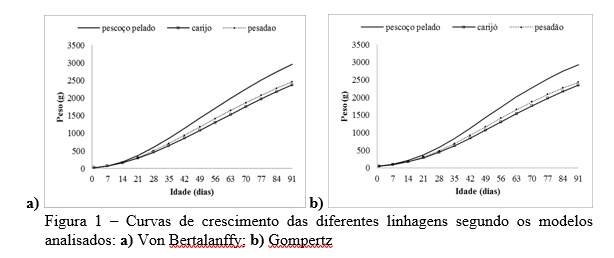
O experimento foi conduzido no setor de avicultura da Escola de Medicina Veterinária e Zootecnia (EMVZ) da Universidade Federal do Tocantins (UFT). Utilizando-se 90 aves caipiras, sendo 30 aves de cada uma das seguintes linhagens: Pescoço Pelado, Carijó e Pesadão Vermelho, obtidas no comércio local. Os pintos de um dia foram pesados e divididos por linhagem em baterias metálicas dotadas de gaiolas experimentais, localizadas no interior do galpão convencional equipadas com comedouros e bebedouros do tipo calha. Aos 29 dias de idade as aves foram transferidas para os piquetes, seguindo a mesma divisão. As rações experimentais, composta basicamente por milho moído e farelo de soja e adquiridas em comercio local para atender as exigências nutricionais das aves de acordo com a fase de criação. O peso corporal individual dos frangos foi medido semanalmente até os 91 dias de idade. Para a determinação das curvas de crescimento do peso corporal das aves, os dados coletados foram avaliados por meio dos modelos de crescimento: Gompertz: y=a*exp(-b*exp(-k*idade)); Bertalanffy: y=a*(1-b*exp(-k*idade))**3; As análises estatísticas foram realizadas utilizando-se o procedimento para análise de modelos não lineares (PROC NLIN) do software Statistical Analysis System (SAS, 2002), por meio do método interativo de Gauss-Newton. Os critérios usados para escolha do modelo de melhor ajuste da curva de crescimento foram o coeficiente de determinação (R²), calculado pela função 1 - (SQR/SQTc), sendo SQR a soma de quadrados do resíduo e SQTc a soma de quadrados total corrigida pela média. O desvio padrão assintótico (DPA), calculado a partir da raiz quadrada do quadrado médio do resíduo de cada modelo. O desvio médio absoluto (DMA), calculado de acordo com a fórmula proposta por Sarmento et al (2006). Para a escolha do melhor modelo, foi utilizado o índice assintótico (IA), descrito por Ratkowsky (1990), combinando os critérios DPA, DMA e R2, atribuindo valor 100 para a maior estimativa de cada critério, sendo os demais ponderados em relação a este, assim: IA= (DPA+DMA) - R². Quanto menor o índice, melhor o ajuste do modelo.Resultados e Discussão
De acordo com a regulamentação do DIPOA n.º 02/2012 (BRASIL, 2012), o peso de abate de frangos caipiras é 2,300kg, sendo assim a linhagem pescoço pelado (PP), foi a que levou menor tempo para atingir a idade de abate, seguida da linhagem pesadão e carijó (tabela 1). Tabela 1. Média dos pesos corporais (g) em diferentes idades para as linhagens (L) pescoço pelado (PP), carijó (CJ) e pesadão (PD).| L | Peso Corporal em (g) | ||||||||||||||
| 1 dia | 7 dias | 14 dias | 21 dias | 28 dias | 35 dias | 42 dias | 49 dias | 56 dias | 63 dias | 70 dias | 77 dias | 84 dias | 91 dias | ||
| PP | 28,2 | 87,1 | 206,8 | 385,5 | 599,6 | 834,4 | 1107,2 | 1420,7 | 1696, 2 | 2000,7 | 2245,8 | 2497,7 | 2723, 2 | 2899,5 | |
| CJ | 34,6 | 85,0 | 176,9 | 307,4 | 646,6 | 622,5 | 837,0 | 1064,0 | 1298,0 | 1552,0 | 1772,0 | 1984,0 | 2196,0 | 2331,0 | |
| PD | 35,5 | 82,1 | 177,6 | 325,0 | 500,5 | 682,8 | 931,2 | 1093,4 | 1428,6 | 1663,3 | 1874,5 | 2089,1 | 2250,3 | 2449,8 | |
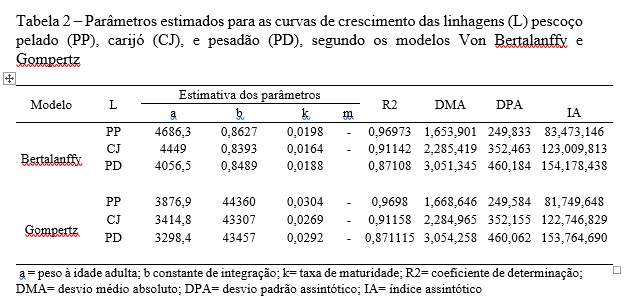
| Modelo | L | Estimativa dos parâmetros | R2 | DMA | DPA | ||||
| a | b | k | m | IA | |||||
| Bertalanffy | PP | 4686,3 | 0,8627 | 0,0198 | - | 0,96973 | 1,653,901 | 249,833 | 83,473,146 |
| CJ | 4449 | 0,8393 | 0,0164 | - | 0,91142 | 2,285,419 | 352,463 | 123,009,813 | |
| PD | 4056,5 | 0,8489 | 0,0188 | 0,87108 | 3,051,345 | 460,184 | 154,178,438 | ||
| Gompertz | PP | 3876,9 | 44360 | 0,0304 | - | 0,9698 | 1,668,646 | 249,584 | 81,749,648 |
| CJ | 3414,8 | 43307 | 0,0269 | - | 0,91158 | 2,284,965 | 352,155 | 122,746,829 | |
| PD | 3298,4 | 43457 | 0,0292 | - | 0,871115 | 3,054,258 | 460,062 | 153,764,690 | |
Conclusões
Entre os modelos analisados, Gompertz e von Bertalanffy, se ajustaram bem ao crescimento das linhagens estudadas. O modelo Gompertz mostrou-se o mais adequado, por conter menor IA destacando o modelo de melhor ajuste. A linhagem que apresentou maior taxa de crescimento foi a pescoço pelado, confirmando sua ótima adaptação para produção na região norte do Tocantins.Gráficos e Tabelas