Modelos matemáticos (Logístico e Richards) para determinar o crescimento de três linhagens de frangos caipira

Mathematical models (Logístico and Richards) to determine the growth of three lineages chickens caipira

ABSTRACT - The objective of this study was to identify, by means of different statistical criteria, the adjustment of the nonlinear regression model most adequate to describe the growth curve of three lines of slow growing chickens. A total of 90 birds were used, of which 30 birds were from each of the following lineages: Pescoço pelado, Carijó and Pesadão Vermelho. The individual body weight of chickens was collected weekly to determine the growth curves using Logistic and Richards models. Among the models evaluated, the logistic model proved to be the most appropriate, since it contained a lower asymptotic index, showing the best fit model.

---

Introdução

Na avicultura é de extrema importância conhecer o padrão e o potencial de crescimento das aves, expresso em peso corporal e ganho de peso, visto que é variável de acordo com a espécie ou genética, idade, e os fatores ambientais que podem influenciar na resposta biológica. O padrão de crescimento dos animais pode ser representado por curvas de crescimento, que é o uso de modelos para a descrição matemática de fenômenos biológicos, assim, variáveis quantitativas são tomadas para representar fatores que influenciam o fenômeno, sendo que a informação contida em um número de pontos, dados pelas coordenadas de peso e tempo, pode ser sumarizada em poucos parâmetros com intepretação biológica, fornecendo estimativas de taxa de crescimento, grau de maturidade e tamanho a maturidade (RONDON et al., 2002; LAIRD & HOWARD, 1967). Além de melhorar os índices produtivos, o estudo da curva de crescimento possibilita uma melhor avaliação da população, permitindo o planejamento e alterações na curva de crescimento dos animais, por meio de seleção e otimização das estratégias de alimentação, priorizando as necessidades nutricionais em cada fase de crescimento (GOUS,1998). Desse modo, objetivou-se identificar, por meio de diferentes modelos matemáticos, o ajuste do modelo de regressão não linear mais adequado para descrever a curva de crescimento de três linhagens de frangos de crescimento lento.

---

Revisão Bibliográfica

O conhecimento dos fatores que influenciam o desenvolvimento corporal do animal é fundamental para compreender como as técnicas de manejo adotadas podem interferir tanto no crescimento como no desempenho do animal (PATINÕ; VAN CLEEF, 2010). Os tecidos musculares e adiposo apresentam ordem diferentes de deposição no corpo, com ação direta de efeitos como genética, sexo e alimentação, de modo que avaliação do crescimento permite identificar quais animais terão melhor conformação e desenvolvimento corporal, com melhor desempenho na sua fase adulta (MOTA et. al, 2014). As aves caipiras são resultados de programas de melhoramento genético, sendo trabalhadas geneticamente, selecionadas e adaptadas para a fixação de alguns fatores produtivos, ao mesmo tempo, reduzindo características indesejáveis, compondo no decorrer do tempo um sistema que permite obter boa produtividade. (SANTOS; RIBEIRO; CARVALHO, 2009). Encontra-se no mercado, linhagens específicas para produção de carne, ovos e de dupla aptidão, o que acarreta facilidade ao produtor no momento da escolha da linhagem diminuindo o custo de produção (CUNHA FILHO, 2014). Dessa maneira, a escolha pela linhagem vai depender de 3 fatores fundamentais: o objetivo da criação, a disponibilidade do produto na região e sua capacidade de adaptação (MAIA, 2012).

---

Materiais e Métodos

O experimento foi conduzido no setor de avicultura da Escola de Medicina Veterinária e Zootecnia (EMVZ) da Universidade Federal do Tocantins (UFT), município de Araguaína região norte do Tocantins. Utilizando-se 90 aves caipiras, sendo 30 aves de cada uma das seguintes linhagens:  Pescoço Pelado, Carijó e Pesadão Vermelho, obtidas no comércio local. Os pintos de um dia foram pesados e divididos por linhagem em baterias metálicas dotadas de gaiolas experimentais (1,00x1,00x0,40m) localizadas no interior do galpão convencional (8 x 6m), equipadas com comedouros e bebedouros do tipo calha e sistema de iluminação para aquecimento das aves. Aos 29 dias de idade as aves foram transferidas para os piquetes, seguindo a mesma divisão, em cada piquete continha um abrigo, coberto com palha de babaçu, com bebedouro pendular e comedouro tubular. As rações experimentais, composta por milho moído, farelo de soja, sorgo baixo tanino, premix mineral vitamínico e calcário calcitico, foram adquiridas em comercio local para atender as exigências nutricionais das aves na fase inicial (1 a 28 dias), crescimento, (29 a 56 dias) e terminação (57 a 91 dias). O peso corporal individual dos frangos foi medido semanalmente, (1, 7, 14, 21,28, 35, 42, 49, 56, 63, 70, 77, 84 e 91 dias de idade). Para a determinação das curvas de crescimento do peso corporal das aves, os dados coletados foram avaliados por meio dos modelos de crescimento: Logistico:        y=a*((1+b*exp(-k*idade))**-1); Richards:         y=a*(1-b*(exp(-k*idade)))**m; As análises estatísticas foram realizadas utilizando-se o procedimento para análise de modelos não lineares (PROC NLIN) do software Statistical Analysis System (SAS, 2002), por meio do método interativo de Gauss-Newton. Os critérios usados para escolha do modelo de melhor ajuste da curva de crescimento foram o coeficiente de determinação (R²), calculado pela função 1 - (SQR/SQTc), sendo SQR a soma de quadrados do resíduo e SQTc a soma de quadrados total corrigida pela média. O desvio padrão assintótico (DPA), calculado a partir da raiz quadrada do quadrado médio do resíduo de cada modelo. O desvio médio absoluto (DMA), calculado de acordo com a fórmula proposta por Sarmento et. al., (2006). Para a escolha do melhor modelo, foi utilizado o índice assintótico (IA), descrito por Ratkowsky (1990), combinando os critérios DPA, DMA e R2, atribuindo valor 100 para a maior estimativa de cada critério, sendo os demais ponderados em relação a este, assim: IA= (DPA+DMA) - R². Quanto menor o índice, melhor o ajuste do modelo.

---

Resultados e Discussão

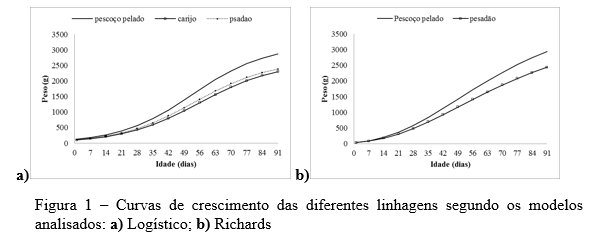
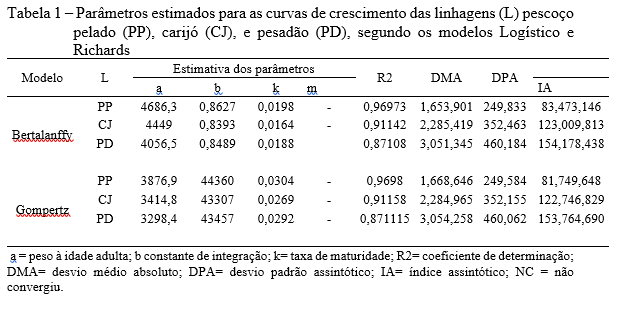
A equação proposta pelo modelo Logístico convergiu para todas as linhagens avaliadas, enquanto a análise realizada pelo Modelo Richards só convergiu para a linhagem pescoço pelado e pesadão, para a linhagem carijó não convergiu, mostrando que este modelo não se adequa a descrição dos pesos desta linhagem (tabela 1).   Tabela 1 – Parâmetros estimados para as curvas de crescimento das linhagens (L) pescoço pelado (PP), carijó (CJ), e pesadão (PD), segundo os modelos Logístico e Richards

Modelo	L	Estimativa dos parâmetros				R2	DMA	DPA
		a	b	k	m				IA
Bertalanffy	PP	4686,3	0,8627	0,0198	-	0,96973	1,653,901	249,833	83,473,146
	CJ	4449	0,8393	0,0164	-	0,91142	2,285,419	352,463	123,009,813
	PD	4056,5	0,8489	0,0188		0,87108	3,051,345	460,184	154,178,438
Gompertz	PP	3876,9	44360	0,0304	-	0,9698	1,668,646	249,584	81,749,648
	CJ	3414,8	43307	0,0269	-	0,91158	2,284,965	352,155	122,746,829
	PD	3298,4	43457	0,0292	-	0,871115	3,054,258	460,062	153,764,690

a = peso à idade adulta; b constante de integração; k= taxa de maturidade; R2= coeficiente de determinação; DMA= desvio médio absoluto; DPA= desvio padrão assintótico; IA= índice assintótico; NC = não convergiu.   Nos dois modelos estudados, o parâmetro “a” (peso à idade adulta) apresentou maior valor para o pescoço pelado. Esse resultado mostra que as aves da linhagem pescoço pelado tendem a apresentar o maior peso à idade adulta e as aves da linhagem carijó, que apresentaram menor valor de “a” no modelo Logístico, tendem a menor peso à maturidade. No modelo logístico os valores de “a” da linhagem carijó e pesadão são próximos. O parâmetro “k” representa a velocidade com que o animal passa pelo período de crescimento até se tornar adulto. Nos modelos estudados o valor de “k” é maior para o pescoço pelado, indicando maior taxa de crescimento, e menor para o carijó, indicando menor taxa de crescimento. Verificou-se na linhagem pescoço pelado melhor ajuste aos modelos, pois os valores do desvio médio absoluto (DMA), desvio padrão assintótico (DPA) e de índice assintótico (IA) foram menores, já a linhagem pesadão apresentou os maiores valores de DMA, DPA e IA, indicando pior ajuste aos modelos. O menor valor de IA para as três linhagens estudadas foi observado no modelo Logístico, apontado como o modelo que melhor se ajustou, uma vez que o IA é um critério que leva em consideração o R2, o DMA e DPA, dessa forma um dos critérios mais completo e por isso mais recomendado para a escolha do modelo. Veloso et al (2015) analisou os modelos de curvas de crescimento para as linhagens pescoço pelado, pesadão vermelho, tricolor, carijó e colorpak e verificou que entre os modelos estudados: Richards, Brody, Gompertz, Bertalanffy e Logistico o que melhor se ajustou foi o modelo Bertalanffy. Diferindo dos resultados encontrados no presente trabalho, onde o modelo que apresentou melhor ajuste foi o modelo Logístico. As linhagens apresentaram taxa de crescimento semelhante até os 14 dias de idade (Figura 1), no entanto, após esse período observa-se maior taxa de crescimento para pescoço pelado, devido a sua capacidade de adaptação em regiões de clima quente e a genética da linhagem. Em seguida, o pesadão, e por último a linhagem carijó, com menor taxa de crescimento, provavelmente por ser uma ave de dupla aptidão (carne e ovos). Figura 1 – Curvas de crescimento das diferentes linhagens segundo os modelos analisados: a) Logístico; b) Richards

---

Conclusões

Entre os modelos analisados, o modelo de Richards não se ajustou para linhagem carijó. Os modelos utilizados no presente trabalho se ajustaram bem ao crescimento das linhagens estudadas. O modelo Logístico mostrou-se o mais adequado, por conter menor IA evidenciando o modelo de melhor ajuste.

---

Gráficos e Tabelas

---

Referências

CUNHA FILHO, O. G. da. Curvas de crescimento de frangos caipiras submetidos a diferentes níveis de lisina digestível. 2014. 67f. Dissertação, (mestrado em Zootecnia) – Universidade Federal de Sergipe, 2014.   GOUS, R.M. Lysine: making progress in the nutrition of broilers. Poultry Science, v.77, n.1, p.111-117, 1998.   LAIRD, A.K.; HOWARD, A. Growth curves in imbred mice. Nature, v.213, n.5078, p.786-788, 1967.   MAIA, George André Rodrigues. Avicultura Alternativa: carne e ovos pelo sistema de pastejo. Portal RuralSoft, Minas Gerais, set. 2012. Disponível em:  http://www.ruralsoft.com.br/manejo/manejoExibe.asp?id=87#.VuYYLPkrLIV> Acesso em 27 jan. 2016.     MOTA, L. F. M.; PIRES, A.V.; MARIZ, T.M.de A.; RIBEIRO, J. do S.; BONAFÉ, C.M. Estrutura corporal (Frame Size) e influencias no desempenho produtivo de bovinos de corte. Boletim Técnico PPGZOO,v.2, nº 1, Universidade Federal de Viçosa (UFVJM), Maio/2014.   PATINÕ, P. R.; VAN CLEEF, E. ASPECTOS CHAVE DO CRESCIMENTO EM OVINOS. Rev. Colombiana cienc. Animal (2).2010.   RATKOWSKY, D.A. Handbook of nonlinear regression models. New York and Basel, Marcel Dekker, 1990.   RONDON, E.O.O. et al. Modelagem computacional para produção e pesquisa em avicultura. Revista Brasileira de Ciência Avícola, v.4, n.1, p. 199-207, 2002.   SANTOS, M. W.; RIBEIRO, A. G. P.; CARVALHO, L. S. Criação de galinha caipira para produção de ovos em regime semi-intensivo. Programa Rio Rural, Superintendência de Desenvolvimento Sustentável, Secretaria de Estado de Agricultura, Pecuária, Pesca e Abastecimento, Niterói. 30p, 2009   SARMENTO, J.L.R.; REGAZZI, A.J.; SOUZA, W.H.; TORRES, R. de A.; BREDA, F. C.; MENEZES, G. R. de O. Estudo da curva de crescimento de ovinos Santa Inês. Revista Brasileira de Zootecnia, v. 35, n.2, p.435-442, 2006.   SAS - statistical analysis systems: user’s guide. Version 9.1, Cary: SAS, 2002. v.2, 1052p.   VELOSO, R. C.; PIRES, A.V.; TORRES FILHO, R. A.; DRUMOND, E. C. S.; COSTA, L. S.; AMARAL, J. M.; PEREIRA, I. G. Crescimento de genótipos de frangos tipo caipira. Arquivo Brasileiro de Medicina Veterinária e Zootecnia, v.67, n.5, p.1361-1371, 2015.